(백준) 2644 – 학위계산

문제

솔루션 프로세스

예제 입력 1과 2의 차수 관계 그래프는 다음과 같습니다.

(예제 1, 2와 같이)

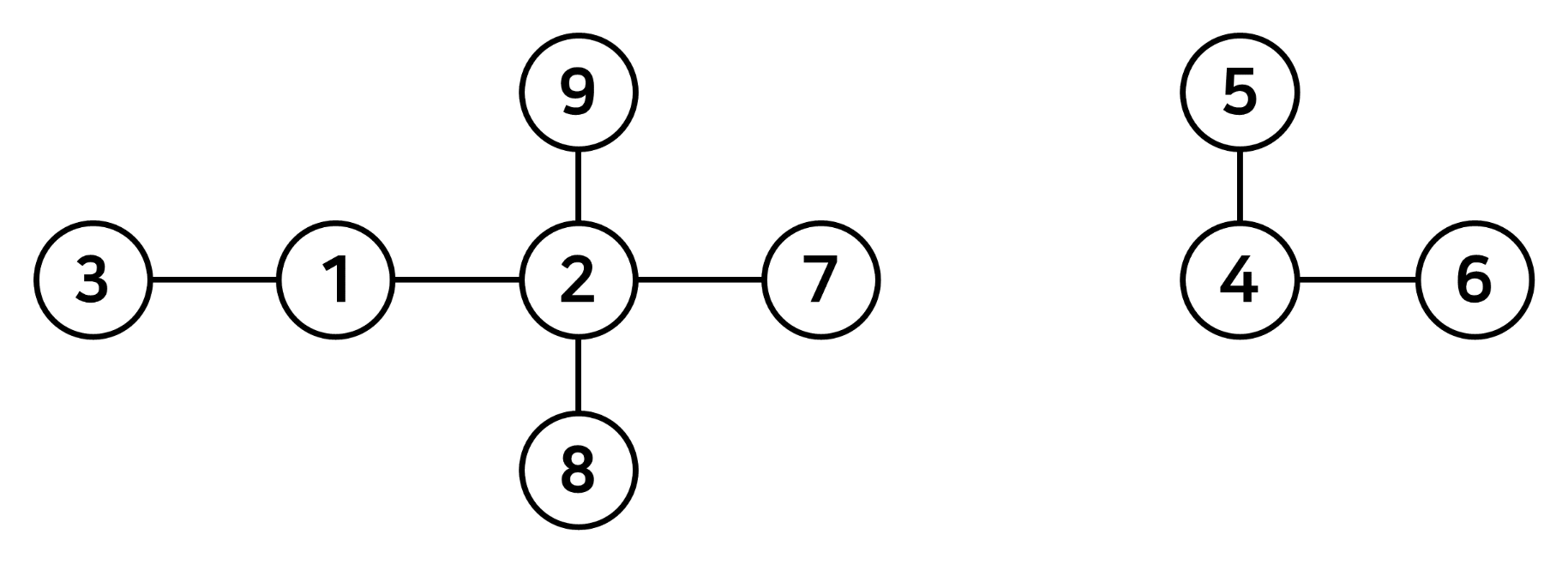
여기서 a에서 b로 가는 모서리의 수는 a와 b의 차수입니다.

예 1) 7과 3의 차수는? 삼

예2) 8과 6의 차수는? 전혀 관계가 없습니다.

① DFS로 해결하세요.

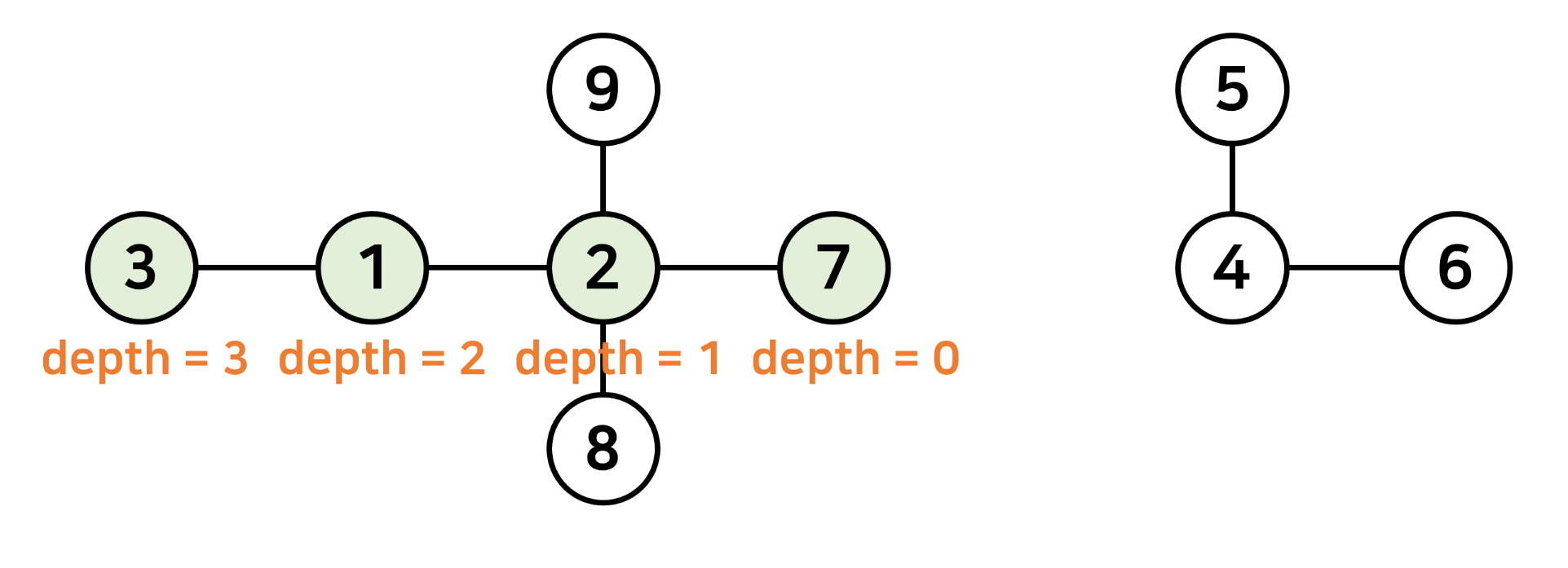
② DFS를 수행할 때 단순히 정점을 방문하는 것이 아니라 현재 깊이를 나타내는 깊이 요소를 추가합니다.

깊이는 시작 노드에서 0이고 선을 넘을 때마다 1씩 증가합니다.

사진 참조 (출발 7시, 도착 3시 답은 3)

답변

import java.io.*;
import java.util.StringTokenizer;

public class Main {

    static int n, from, to;
    static int depth = 0;
    static int()() matrix;
    static boolean() visited;
    static int answer = -1;

    public static void main(String() args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st;

        //첫째 줄 입력, 인접 행렬, 방문 배열 크기 지정
        n = Integer.parseInt(br.readLine());
        matrix = new int(n+1)(n+1);
        visited = new boolean(n+1);

        //두번째 줄 입력
        st = new StringTokenizer(br.readLine());
        from = Integer.parseInt(st.nextToken());
        to = Integer.parseInt(st.nextToken());

        //세번째 줄 입력
        int m = Integer.parseInt(br.readLine());

        //m개의 관계 입력받기, 인접행렬에 추가
        for(int i = 0; i < m; i++){
            st = new StringTokenizer(br.readLine());
            int x = Integer.parseInt(st.nextToken());
            int y = Integer.parseInt(st.nextToken());

            matrix(x)(y) = 1;
            matrix(y)(x) = 1;
        }

        answer = -1;

        DFS(from, depth);

        bw.write(answer + "\n");
        bw.flush();
        bw.close();

    }

    static void DFS(int s, int d){
        if(s == to){
            answer = d;
            return;
        }

        if(visited(s)){
           return;
        } else{
            visited(s) = true;
            for(int i = 1; i <= n; i++){
                if((matrix(s)(i) == 1) && (visited(i) == false))
                    DFS(i, d+1);
            }
        }
    }

}

​​알고리즘 분류

– 그래프 이론

– 다이어그램 탐색

– 너비 우선 검색

– 깊이 우선 탐색 우선